محاسبات سمبلیک چیست؟
محاسبات سمبلیک (Symbolic Cumputation) مربوط به محاسبات ریاضی به صورت سمبلیک میشود و این بدان معناست که محاسبات به صورت دقیق صورت میگیرد و نه تقریبی و عبارات ریاضی به صورت سمبلیک در این محاسبات نمایش داده می شوند.
اجازه بدهید که یک مثال بزنیم. فرض کنید که بخواهیم ریشه یک عدد را محاسبه کنیم. کد آن به صورت زیر می شود:
>>> import math>>> math.sqrt(9)3.0
از آنجا که ۹ یک جذر کامل است بنابراین جواب دقیقاً ۳ می شود. ولی فرض کنید که بخواهیم ریشه یک عدد مثل ۸ که جذر کامل نیست را محاسبه کنیم:
>>> math.sqrt(8)2.82842712475
در اینجا ما جواب تقریبی میگیریم. ۲.۸۲۸۴۲۷۱۲۴۷۵ ریشه دقیق عدد ۸ نیست( درسته که ریشه دقیق عدد ۸ قابل محاسبه نیست، چون یک عدد گنگ است). اگر منظور ما همین عدد اعشاری باشد به مقصود خود رسیده ایم. ولی فرض کنید که ما میخواهیم جوابی شبیه زیر بگیریم:
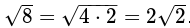
زمان زیادی لازم دارد تا ما به این فرم از نتیجه برسیم و این زمانی است که محاسبات سمبلیک به کمک ما می آید، بنابراین با استفاده از sympy نتیجه به صورت زیر خلاصه میگردد:
>>> sympy.sqrt(8) 2*sqrt(2)
قدرت محاسبات سمبلیک:
قدرت واقعی سیستمهای محاسبات سمبلیک شبیه به sympy این است که تمام انواع محاسبات را به صورت سمبلیک انجام دهند. Sympy میتواند مشتق، انتگرال و حد را محاسبه کند، معادلات را حل کند. همچنین توانایی کار با ماتریسها و بسیاری کارهای دیگر را به صورت سمبلیک دارد.اینها نمونههایی از قدرت sympy است برای اینکه اشتهای شما را تحریک کند!
>>> from sympy import * >>> x, t, z, nu = symbols('x t z nu')
مشتق
تابع 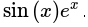
>>> diff(sin(x)*exp(x), x) x x ℯ ⋅sin(x) + ℯ ⋅cos(x)
محاسبه
انتگرال 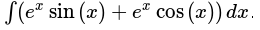
>>> integrate(exp(x)*sin(x) + exp(x)*cos(x), x) x ℯ ⋅sin(x)
حل
معادله دیفرانسیل 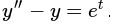
>>> y = Function('y') >>> dsolve(Eq(y(t).diff(t, t) - y(t), exp(t)), y(t))
پرینت
تابع 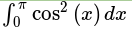 توسط
نرمافزار LATEX
توسط
نرمافزار LATEX
>>> latex(Integral(cos(x)**2, (x, 0, pi))) \int_{0}^{\pi} \cos^{2}{\left (x \right )}\, dx
برای کسب اطلاعات بیشتر در مورد نرم افزارهای محاسبات سمبلیک به این ویکی مراجعه کنید.
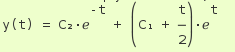



عالی بود . ممنون